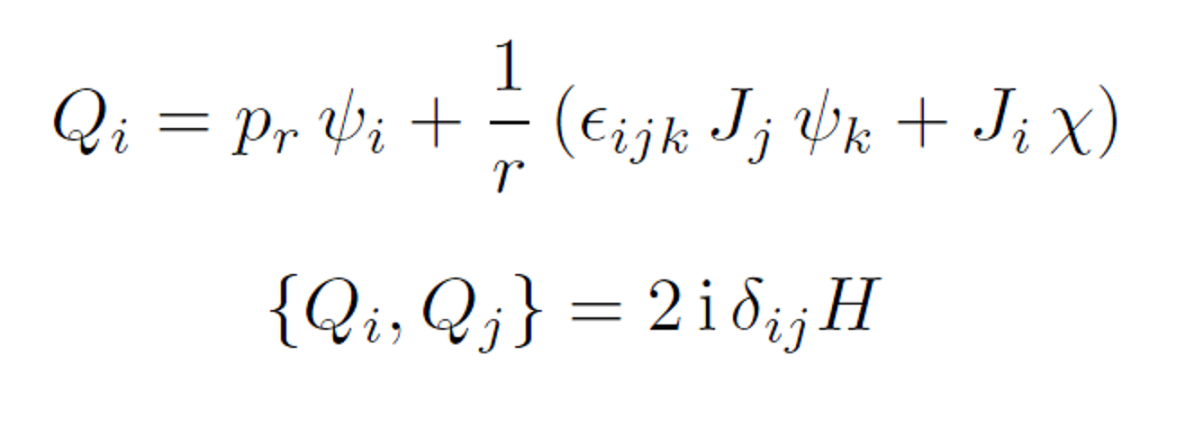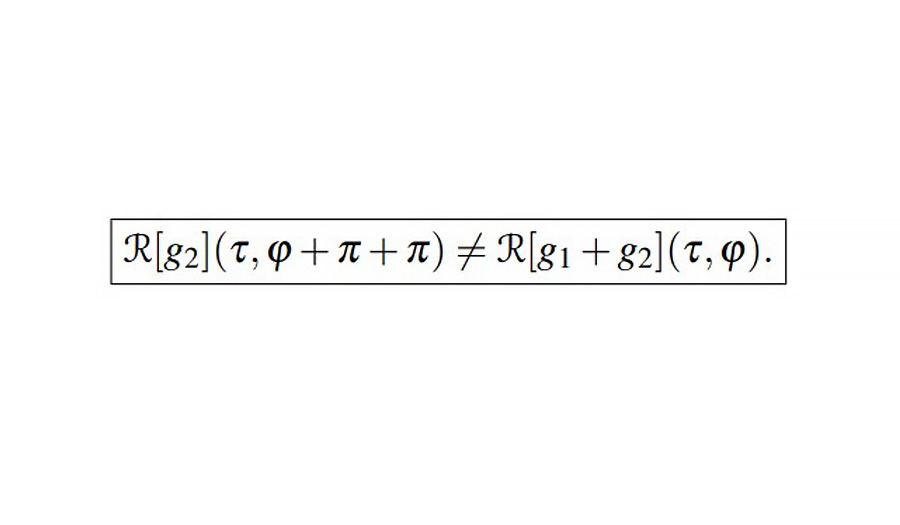This introductory review is devoted to the newest section of the theory of symmetries -- the theory of quantum groups.
The principles of the theory of quantum groups are reviewed from the point of view of the possibility of their use for deformations of symmetries in physics models. The R-matrix approach to the theory of quantum groups is discussed in detail and is taken as the basis of the quantization of classical Lie groups, as well as some Lie supergroups. We start by laying out the foundations of non-commutative and non-cocommutative Hopf algebras. Much attention has been paid to Hecke and Birman-Murakami-Wenzl (BMW) R-matrices and related quantum matrix algebras. Noncommutative differential geometry on quantum groups of special types is discussed. Trigonometric solutions of the Yang-Baxter equations associated with the quantum groups GLq(N), SOq(N), Spq(2n) and supergroups GLq(N|M), Ospq(N|2m), as well as their rational (Yangian) limits, are presented. Rational R-matrices for exceptional Lie algebras and elliptic solutions of the Yang-Baxter equation are also considered. The basic concepts of the group algebra of the braid group and its finite dimensional quotients (such as Hecke and BMW algebras) are outlined. A sketch of the representation theories of the Hecke and BMW algebras is given, including methods for finding idempotents (quantum Young projectors) and their quantum dimensions. Applications of the theory of quantum groups and Yang-Baxter equations in various areas of theoretical physics are briefly discussed.
This is a modified version of the review paper published in 2004 as a preprint of the Max-Planck-Institut für Mathematik in Bonn.
We construct superconformal mechanics with N = 3 and N = 4 supersymmetries that were inspired by analogy with the supersymmetric Schwarzian mechanics. The Schwarzian, being another system with superconformal symmetry, provides insight into the field content of supersymmetric mechanics, most notably, on the number and properties of the fermionic fields involved. Adding more fermionic fields (four in the N = 3 case and eight in the N = 4 case) made it possible to construct systems possessing maximal superconformal symmetries in N = 3 and N = 4, namely osp(3|2) and D(1, 2; α). In the case of N = 4 supersymmetry, we explicitly construct a new variant of N = 4 superconformal mechanics in which all bosonic subalgebras of the D(1, 2; α) superalgebra have a bosonic realization. In addition, the constructed systems involve the so(3) currents whose parameterization is not fixed, which allows one to consider different underlying geometries.
For the reconstruction problem, the universal representation of inverse Radon transforms implies the needed complexity of the direct Radon transforms which leads to additional contributions. In the standard theory of generalized functions, if the outset (origin) function which generates the Radon image is a pure-real function, as a rule, the complexity of Radon transforms becomes in question. In the paper, we discuss the Fourier slice theorem analyzing the degenerated (singular) points as possible sources of the complexity. We also demonstrate different methods to generate the needed complexity at the intermediate stage of calculations. Besides, we show that the introduction of the hybrid (Wigner-like) function ensures naturally the corresponding complexity. The discussed complexity not only provides the additional contribution to the inverse Radon transforms, but also makes an essential impact on the reconstruction and optimization procedures within the framework of the incorrect problems. The presented methods can be effectively used for the practical tasks of reconstruction problems.
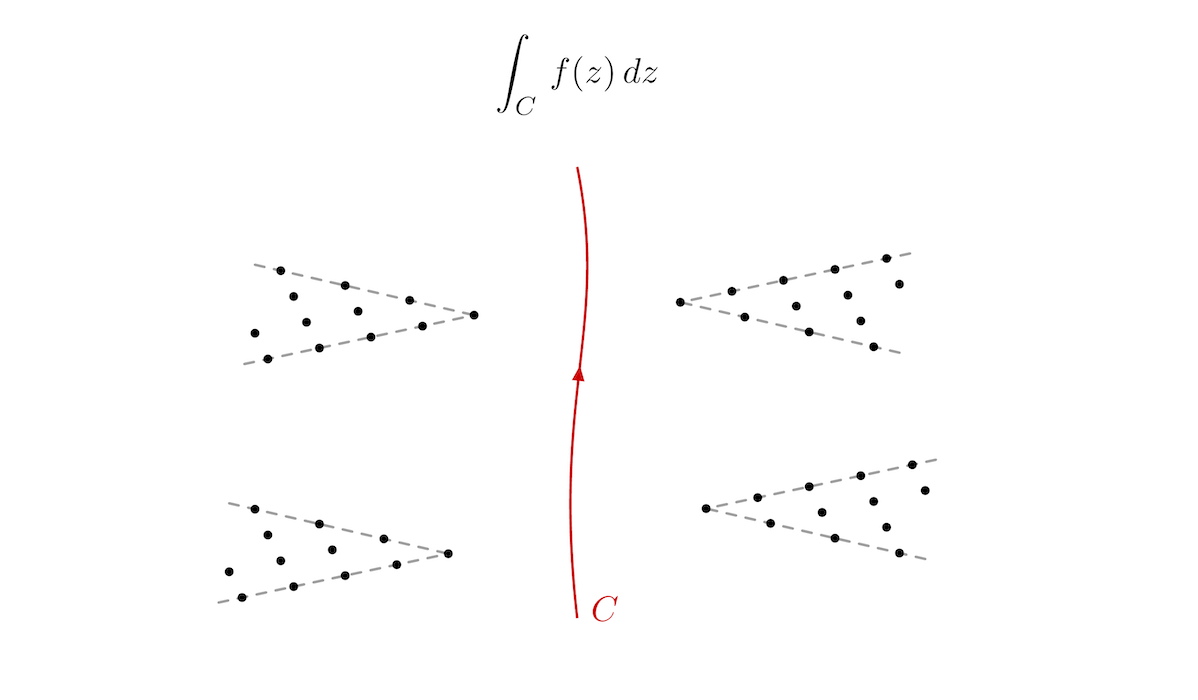
We consider a complex rational degeneration of the hyperbolic Ruijsenaars model emerging in the limit ω1 + ω2 → 0 (or b → i in 2d CFT) and investigate the two-particle case in detail. Corresponding wave functions are described by complex hypergeometric functions in the Mellin–Barnes representation. Their dual integral representation and reflection symmetry in the coupling constant are established. Besides, a complex limit of the hyperbolic Baxter Q-operators is considered. Another complex degeneration of the hyperbolic Ruijsenaars model is obtained by taking a special ω1 − ω2 → 0 (or b → 1) limit. Additionally, two new degenerations to the complex Calogero–Sutherland type models are described.