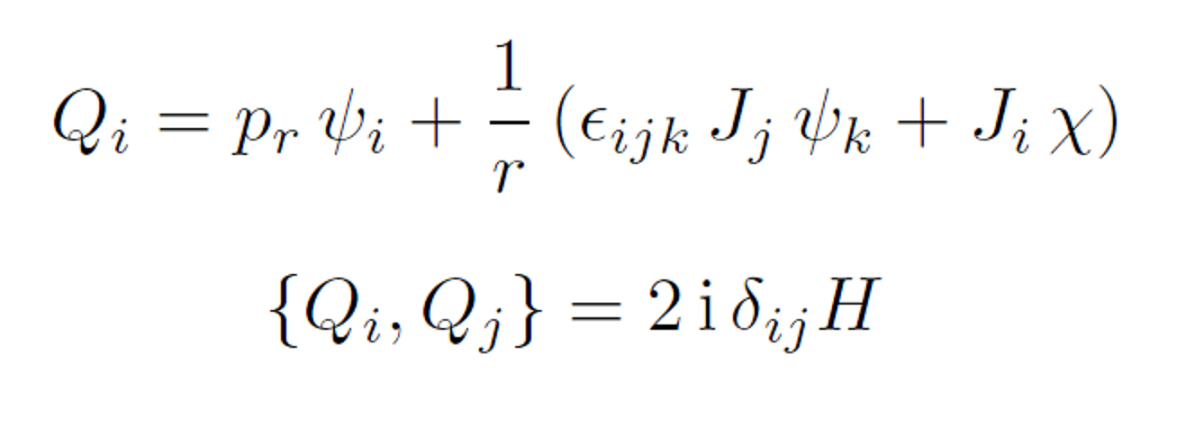Выпуск 5 (Том 2) 2025

С использованием аналогии с суперсимметричными Шварцевыми механиками, построены суперконформные механики с N = 3 и N = 4 суперсимметрией. Шварциан, будучи системой с суперконформной симметрией, способствует пониманию состава полей суперсимметричной механики, особенно числа и свойств фермионных полей. Добавление большего числа фермионных полей (четырех для N = 3 и восьми для N = 4) позволяет построить системы, обладающие максимальной суперконформной симметрией: osp(3|2) для N = 3 и D(1, 2; α) для N = 4. В случае N = 4 суперсимметрии, построен новый вариант суперконформной механики, в котором все бозонные подалгебры D(1, 2; α) имеют бозонную реализацию. Параметризация so(3) токов, входящих в построенные системы, не фиксирована, что позволяет рассматривать различные варианты геометрии таких механик.

Данный краткий обзор посвящён празднованию двух важнейших событий в квантовой физике: появлению концепции о конденсации Бозе-Эйнштейна (1925) и её экспериментальному подтверждению, которое установило, что конденсация действительно существует и возникает в жидком ⁴Не одновременно с появлением сверхтекучести ниже температуры λ-точки (1975).

Оба эти события тесно связаны с теорией сверхтекучести Н. Н. Боголюбова (1947), поскольку ключевой гипотезой этой теории является наличие конденсата в системе взаимодействующих бозонов. Таким образом, эксперименты, начатые в ОИЯИ (Дубна), подтвердили в 1975 году предсказание теории Боголюбова о том, что сверхтекучесть жидкого ⁴Не (He II) должна возникать одновременно с конденсатом Бозе-Эйнштейна.

Исправлено:
13 ноября 2025 (подписи к рисункам 1 и 2 были изменены)
26 ноября 2025 (были внесены изменения в формулы (53) и (55))

Рассматривается комплексное рациональное вырождение гиперболической  модели Руйсенарса, возникающее в пределе ω₁ + ω₂ → 0 (или b → i в 2d конформной теории поля), и детально изучается случай двухчастичной системы. Соответствующие волновые функции описываются  комплексными гипергеометрическими функциями в представлении Меллина-Барнса. Найдены их дуальное интегральное представление и симметрия отражения по константе взаимодействия. Кроме того, рассмотрен комплексный предел гиперболического Q-оператора Бакстера. Другое комплексное вырождение гиперболической модели Руйсенарса получено переходом к специальному пределу ω₁ − ω₂ → 0 (или b → 1). Дополнительно представлены два новых вырождения к комплексным моделям типа Калоджеро-Сазерленда.

Рассмотрена возможность использования синхротрона формы-8 в качестве замены Нуклотрона для ускорения поляризованных протонов и дейтронов в комплексе коллайдера NICA. Арки синхротрона размещены внутри туннеля коллайдера NICA. Представленный инжектор позволяет сохранять поляризацию и осуществлять инжекцию любого сорта частиц (p, d, ³He и др.) в коллайдерные кольца во всем диапазоне энергий. Благодаря своей форме кольцо работает в режиме спиновой прозрачности. Управление направлением поляризации осуществляется с помощью спинового навигатора, использующего слабые соленоидальные поля. Синхротрон также может использоваться в качестве накопительного кольца для высокоточных экспериментов с поляризованными пучками помимо применения в качестве инжектора для коллайдера. В работе приводятся результаты численного моделирования спиновой динамики при ускорении протонов и дейтронов.

В рамках задачи реконструкции универсальное представление обратного преобразования Радона предполагает необходимость в комплексности прямого преобразования Радона, которое ведет к дополнительным вкладам. В стандартной теории обобщенных функций если первоначальная функция, генерирующая радоновский образ, является чисто вещественной функцией, то, как правило, комплексность преобразования Радона становится под вопросом. В данной работе, анализируя вырожденные (сингулярные) точки, обсуждается теорема о разрезах Фурье как возможный источник комплексности. Также продемонстрированы различные методы генерации необходимой комплексности на промежуточных этапах вычислений. Кроме того, показано, что введение гибридной функции подобно функции Вигнера обеспечивает естественным способом соответствующую комплексность. Обсуждаемая комплексность ведет не только к возникновению дополнительного вклада в обратном преобразовании Радона, но и оказывает существенное влияние на задачу о реконструкции и на процедуру оптимизации в рамках некорректных задач. Представленные методы могут быть эффективно использованы в практических решениях задач о реконструкции.