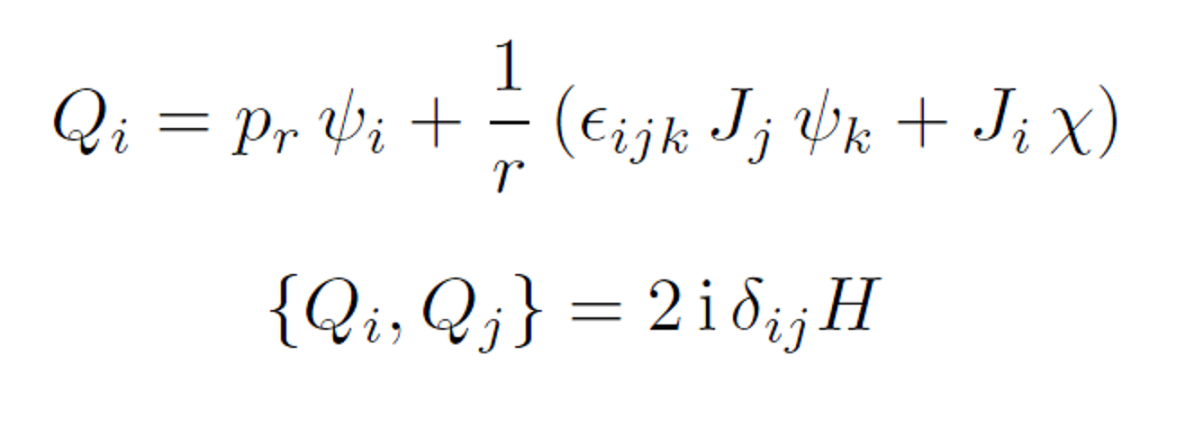Issue 5 (Volume 2) 2025

We construct superconformal mechanics with N = 3 and N = 4 supersymmetries that were inspired by analogy with the supersymmetric Schwarzian mechanics. The Schwarzian, being another system with superconformal symmetry, provides insight into the field content of supersymmetric mechanics, most notably, on the number and properties of the fermionic fields involved. Adding more fermionic fields (four in the N = 3 case and eight in the N = 4 case) made it possible to construct systems possessing maximal superconformal symmetries in N = 3 and N = 4, namely osp(3|2) and D(1, 2; α). In the case of N = 4 supersymmetry, we explicitly construct a new variant of N = 4 superconformal mechanics in which all bosonic subalgebras of the D(1, 2; α) superalgebra have a bosonic realization. In addition, the constructed systems involve the so(3) currents whose parameterization is not fixed, which allows one to consider different underlying geometries.

This short review is devoted to the celebration of two major events in quantum physics. The first one is the birth of the concept of Bose–Einstein condensation (1925) and the second is the experimental proof that it does exist and appears in liquid ⁴He simultaneously with superfluidity below the λ-point (1975).
Both of these events are tightly related to the Bogoliubov theory of superfluidity (1947). The existence of condensate in the system of interacting bosons is the key ansatz of this theory. Therefore, the experiments started at JINR-Dubna in 1975 confirmed this prediction of the Bogoliubov theory that superfluidity of liquid ⁴He (He II) should emerge at the same time as the Bose–Einstein condensation.

Corrected:
13 November 2025 (the captions to Figures 1 and 2 were changed)
26 November 2025 (changes were made in formulas (53) and (55))

We consider a complex rational degeneration of the hyperbolic Ruijsenaars model emerging in the limit ω₁ + ω₂ → 0 (or b → i in 2d CFT) and investigate the two-particle case in detail. Corresponding wave functions are described by complex hypergeometric functions in the Mellin–Barnes representation. Their dual integral representation and reflection symmetry in the coupling constant are established. Besides, a complex limit of the hyperbolic Baxter Q-operators is considered. Another complex degeneration of the hyperbolic Ruijsenaars model is obtained by taking a special ω₁ − ω₂ → 0 (or b → 1) limit. Additionally, two new degenerations to the complex Calogero–Sutherland type models are described.

The paper considers a possibility to use the figure-8 synchrotron as a replacement of the Nuclotron for acceleration of polarized proton and deuteron beams at the NICA accelerator complex. The synchrotron arcs are placed inside the NICA collider tunnel. The presented design enables preservation of polarization for any ion species (p, d, ³He, etc.) in the entire energy range of the synchrotron. Because of its shape, the ring operates in the spin transparency mode. The direction of polarization is controlled by a spin navigator which uses weak solenoidal fields. The synchrotron can also be used as a storage ring for high precision experiments with polarized beams beyond its use as an injector to the collider. The results of numerical simulations of spin dynamics for acceleration of protons and deuterons are presented. 

For the reconstruction problem, the universal representation of inverse Radon transforms implies the needed complexity of the direct Radon transforms which leads to additional contributions. In the standard theory of generalized functions, if the outset (origin) function which generates the Radon image is a pure-real function, as a rule, the complexity of Radon transforms becomes in question. In the paper, we discuss the Fourier slice theorem analyzing the degenerated (singular) points as possible sources of the complexity. We also demonstrate different methods to generate the needed complexity at the intermediate stage of calculations. Besides, we show that the introduction of the hybrid (Wigner-like) function ensures naturally the corresponding complexity. The discussed complexity not only provides the additional contribution to the inverse Radon transforms, but also makes an essential impact on the reconstruction and optimization procedures within the framework of the incorrect problems. The presented methods can be effectively used for the practical tasks of reconstruction problems.